In der heutigen Ausgabe der FAZ am Sonntag gab es mal wieder ein spannendes Rätsel. Dabei ging es in dem Artikel eigentlich gar nicht um das Rätsel. Der Aufhänger des Artikels war der Spruch “In Mathe bin ich Deko.”, den der Otto-Versand wohl auf Mädchen-T-Shirts unters Volk brachte. Dadurch ist es bei Twitter wohl zu einem #aufschrei gekommen und der Otto-Versand nahm das T-Shirt wieder aus dem Versand.
Wie auch immer. Der Artikel endete auf alle Fälle mit der Aufgabe:
Auf der Autobahn hat sich ein Stau gebildet. Ein Überwachungs-Flugzeug überfliegt die Kolonne in 3,5 Minuten und entgegen der Fahrtrichtung in 2,5 MInuten. Die Geschwwindigkeit des Flugzeugs beträgt 200 km/h. Wie lang und wie schnell ist der Stau?
Ergänzen möchte ich noch die Angaben, dass der Stau sich während des Überflugs nicht in der Länge verändert und mit konstanter Geschwindigkeit vorwärts bewegt.
Spontan hat mich das an eine Aufgabe meines Schwagers erinnert, die er mir vor circa einem halben Jahr stellte:
Ein Schäferhund befindet sich am Ende einer 1 km langen Schafherde, die sich mit konstanter Geschwindigkeit vorwärts bewegt.
Zur Kontrolle läuft er nun – mit einer größeren, konstanten Geschwindigkeit als die Herde – vom Ende bis zur Spitze der Herde und wieder an seinen Platz am Ende der Herde zurück. Als er wieder hinten ankommt, ist die Schafherde genau 1 km weiter gewandert. Wie weit ist der Hund gelaufen?
So ähnlich die Aufgaben sind, so unterschiedlich sind die Ergebnisse – denke ich. Die Hundeaufgabe kann man mit Hilfe eines t-s-Diagramms wunderbar lösen: 1+√ 2
Allerdings verhält sich die Stau-Aufgabe bei ähnlichem Ansatz da etwas störrischer. Hier der erste Versuch: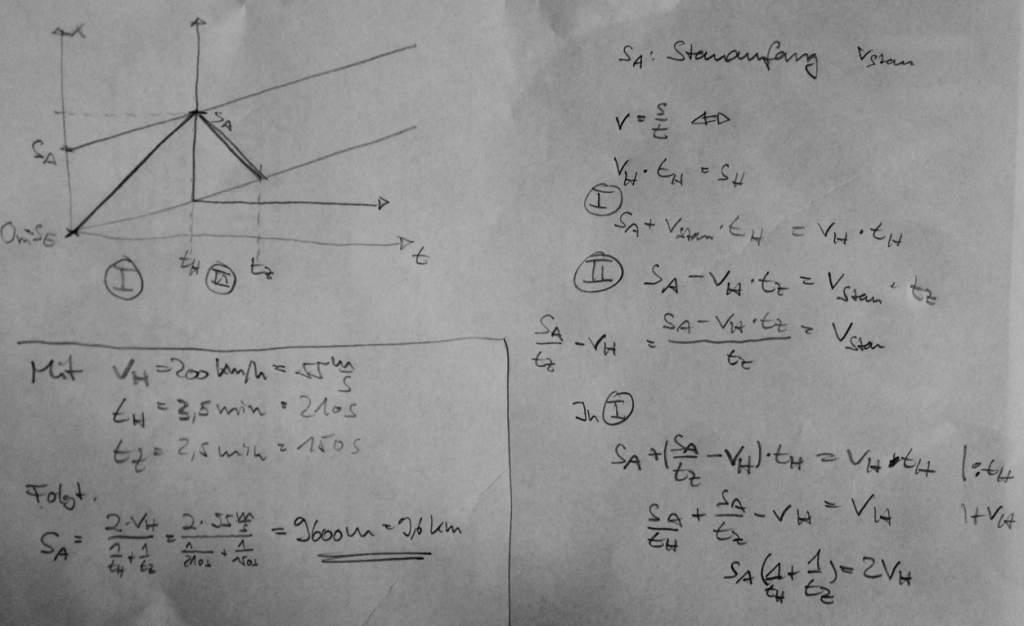
Ergebnis 1: Staulänge * ( 1⁄thin + 1⁄tzurück ) = 2 vFlugzeug
Setzt man alles ein und löst auf, so ergibt sich eine Staulänge von 9,6 km. Dies kann man dann auch benutzen, um die Staugeschwindigkeit auszurechnen.
Wer noch was zum Knobeln braucht, erweitert die Aufgabe zu dieser Aufgabenstellung:
Ein Hund läuft mit mit konstanter Geschwindigkeit um eine Kompanie herum, die sich ebenfalls mit konstanter Geschwindigkeit bewegt. Die Maße der Kompanie-Auftstellung: 50m breit und 100m lang. Wenn der Hund einmal um die Kompanie herum ist, hat sich diese um 100m vorwärtsbewegt. Wie schnell war der Hund?
Nachtrag:
Warum der Otto-Versand nicht einfach noch ein (Jungs)-T-Shirt mit dem Aufdruck
- “In Mathe bin ich nur Deko.”
- “In Musik bin ich nur Deko.”
- “In der Schule bin ich nur Deko.”
- “Zu Hause bin ich nur Deko.”
- “________ bin ich nur Deko.”+Stoff-Stift zum selber ausfüllen,
gemacht hat, habe ich nicht ganz verstanden. Das wäre doch am einfachsten gewesen.
RT @IngoBartling: Wie lang ist der Stau?: In der heutigen Ausgabe der FAZ am Sonntag gab … #math http://t.co/WJl0vXbsac
Hallo Herr Bartling,
ich habe zufällig Ihre Seite gefunden. Meine Tochter hat die Aufgabe heute früh auch gerechnet und kommt auf eine Staulänge von 9722.2222 m.
Mir scheint das zu stimmen da bei einer Staugeschwindigkeit von 33.333 km/h die Kontrolle auch aufgeht. In 210sec fliegt das Flugzeug 11666m und der Stau fährt 1944m, ergibt Staulänge 9722m. In 150sec fliegt das Flugzeug 8333m und der Stau fährt 1389m, ergibt wieder Staulänge 9722m.
Bei Ihrer Lösung bewegt sich der Stau mit verschiedenen Geschwindigkeiten. In 210sec 11666m-9600m=2066m entspricht 35.41km/h und in 150sec 9600m-8333m=1267m entspricht 30.41 km/h. Daher glaube ich Ihr Rechenweg (den ich nicht im Einzelnen nachvollzogen habe) muss einen Fehler drin haben. Bin mal gespannt ob Sie meine AUsführung nachvollziehen können.
Ich wünsche Ihnen noch einen schönen Sonntag Abend
Jürgen Wagner
Zunächst freut mich erstmal, dass es noch andere gibt die solche Aufgaben interessieren.
Nun zu ihrer Lösung. Wie war denn der Lösungsgang ihrer Tochter? Hatte Sie einen einen ähnlichen Ansatz oder einen ganz anderen? Einen ganz anderen fänd ich schon spannend. Dann habe ich natürlich teilweise stark gerundet, da es ja ein Physikaufgabe ist. Ich versuche meinen Schülern i.a. immer klar zu machen, dass Werte wie 9722.2222 m nicht wirklich sinnvoll sind – denn wer kann schon einen Stau auf 0,1 mm genau angeben? Ich habe daher brereits während meiner Rechnung gerundet, was vielleicht zu der Abweichung von rund 120m im Vergleich zu ihrer Lösung geführt hat.
Ich werde mir aber meine Lösung nochmal genauer anschauen und werde dann ggf. noch einen Kommentar ergänzen.
Auf alle Fälle gratuliere ich zu dieser mathematisch interessierten Tochter und wünsche Ihnen beiden eine erfolgreiche Woche.
Hallo Herr Bartling,
ich habe Ihren Ansatz genau durchgerechnet und käme dann auf 9625.06m Staulänge. Am Runden liegt es also nicht.
Sie hat zuerst die Geschwindigkeit berechnet mit der der Stau sich bewegt und hat mir was von GEschwindigkeitsvektoreen erzählt.
Der Ansatz ist 3.5v-3.5w = 2.5v+2.5w wobei v die Geschwindikkeit des Flugzeugs und w die des Staus ist. Wenn man auflöst und für v=200 km/h einsetzt ergibt das 33.33 (Periode) km/h für den Stau.
Damit kann man die STaulänge wie folgt berechnen: Staulänge=(2.5v+2.5w) / 60 = (2.5*200+2.5*33.33) / 60 = 9.722 (Perode) (Kilometer).
Wenn ich das gegenprüfe scheint es mir stimmig: In 210sec 11666.66m-9722.22m=1944.44m entspricht 33.33km/h und in 150sec 9722.22m-8333.33m=1388.89m entspricht ebenfalls 33.33 km/h. Bin mal gespannt was Sie dazu meinen.
Vielen Dank für das Lob über meine Tochter. Sie wird sich heute Abend sicher sehr freuen!
Nochmals Ihren Ansatz mit dem Taschenrechner gerechnet. Hatte vorhin im Zähler die 55 gelassen obwohl es ja 55.55 sind. Dann kommt doch das gleiche Ergebnis raus! Also Ihr Weg passt auch. Sorry für das Missverständnis.
Ein vektorieller Ansatz bzw. ein Ansatz über die Relativgeschwindigkeiten. Sehr schön und vor allem zu meinem viel einfacher. Prima!
Und das mit dem Runden ist einfach immer ein Problem. Man sollte einfach immer so spät wie möglich Runden, dann passen auch die Ergebnisse besser zusammen.
Natürlich ist es nicht sinnvoll, eine Staulänge auf den Millimeter anzugeben – aber es ist fatal, während einer Rechnung zu runden. Es gibt keinen Grund, der dieses Vorgehen rechtfertig und er kann (wie hier eindrucksvoll bewiesen) zu großen Abweichungen beim Endergebnis führen. Des Weiteren sollte ohnehin nicht mit Dezimalzahlen gerechnet werden, sondern mit Brüchen.
Sinnvolles Runden sollte jedenfalls erst im letzten Schritt stattfinden.
Das ist eine typische Dynamik-Klausur im Maschinenbau-Studiengang. Würde man da (und in anderen Klausuren) jeweils Zwischenergebnisse runden, wäre das Studium sehr schnell gelaufen. Man kann die Aufgabe komplett auf Papier (ohne Rechner) lösen: Es ergeben sich für die Geschwindigkeit der Autos im Stau (1/6)*vFlugzeug; für die Staulänge 2100/216 km. Das größte Problem der meisten “Knobler” dürfte sein, den Ansatz zu finden. MfG Maschbauer
Okkaaaaayyyyy – mit der Aufgabe ist ja ganz schön was von der FAZ – und von mir – ausgelöst worden. Mein Ergebnis, wenn ich mir die Kommentare hier und auch in der Zeitung anschaue: Solche Aufgaben machen vielen Spaß. Und … der Umgang mit dem Runden muss mal aufgearbeitet werden. Letzteres hebe ich mir für die kommenden Osterferien auf. Denn auch im Bereich Informatik gibt es da einiges zu beachten … wenn ich da an Ergebnisse wie 3,000000000000001 und ähnliches denke. Hat zwar andere Ursachen führt aber zu ähnlichen Problemen. Und was rechnet man heutzutage eigentlich noch von Hand – zumindest an der Uni.
Ich will ein T-Shirt: “In der Schule bin ich nur Deko”
Okay…auf dieser Kommentarseite bin ich eindeutig nur Deko.