Das Programmieren läuft. Und in meinen Augen recht gut. Nur manche Schüler haben ein wenig Motivationsprobleme und tun sich mit dem vielleicht etwas trockenen, mathematischen Anwendungen schwer. Aber die Steigerung der Schwierigkeit war gut gewählt – immer gerade so, dass es mit ein bisschen Anstrengung zu schaffen war. Und dadurch sind bei manchen schon deutlich mehr als 50 Zeilen Programm-Code zusammen gekommen.
Heute habe ich noch erklärt, wie man Kommentare schreibt und warum. Es sind damit alle geometrischen Grundfunktionen in Bezug auf Flächen und Volumina umgesetzt worden . Jetzt geht es an komplexere geometrische Körper, die die bestehenden Funktionen ausnutzen. Diese Aufgabe stelle ich mal als eigene Informatik-Aufgabe seperat online.
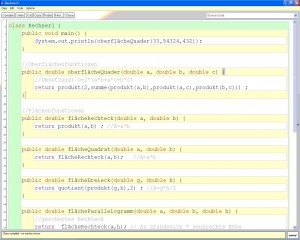
Quelltext
class Rechner1 {
public void main() {
System.out.println(oberflächeQuader(33,54324,432));
}
//Oberflächenfunktionen
public double oberflächeQuader(double a, double b, double c) {
//Umsetzung: O=2*(a*b+a*c+b*c)
return produkt(2,summe(produkt(a,b),produkt(a,c),produkt(b,c))) ;
}
//Flächenfunktionen
public double flächeRechteck(double a, double b) {
return produkt(a,b) ; //A=a*b
}
public double flächeQuadrat(double a, double b) {
return flächeRechteck(a,b); //A=a*b
}
public double flächeDreieck(double g, double h) {
return quotient(produkt(g,h),2) ; //A=g*h/2
}
public double flächeParallelogramm(double a, double b, double h) {
//geschertes Rechteck
return flächeRechteck(a,h); // A: Grundseite * senkrechte Höhe
}
//Grundfunktionen
private double summe(double zahl1, double zahl2) {
return zahl1+zahl2;
}
private double summe(double zahl1, double zahl2, double zahl3) {
return zahl1+zahl2+zahl3;
}
private double differenz(double zahl1, double zahl2) {
return zahl1-zahl2;
}
private double produkt(double zahl1, double zahl2) {
return zahl1*zahl2;
}
private double quotient(double zahl1, double zahl2) {
return zahl1/zahl2;
}
}
Wow, so langsam nimmt ja alles Gestalt an. Klasse! Ich finde es super, dass du keine statics mehr in deinem Programm hast. :)
Kleiner Tipp zur Formatierung: Gönne den Rechenzeichen etwas Luft:
Statt “zahl1+zahl2” lieber “zahl1 + zahl2”.
Auch bei Methodenaufrufen würde ich statt
“flächeRechteck(a,b)” lieber “flächeRechteck(a, b)”
schreiben.
Das finde ich angenehmer zu lesen und wirkt evt. auch für die Schüler etwas aufgeräumter.
Aber sind nur kleine Details. :)
Bei der Formatierung gebe ich dir recht. Ein kleiner Abstand macht es tatsächlich besser. Meistens sieht es eigentlich bei mir so aus:
public double flächeRechteck(double zahl1, double zahl2) {
return produkt(zahl1, zahl2);
}
public double produkt(double zahl1, double zahl2) {
return zahl1 + zahl2;
}
Aber das eigentlich Problem ist eher wie üblich: die Schüler schreiben nur von der Tafel ab, übernehmen aber die Einrückung nicht oder vergessen Klammern oder nehmen die falschen. Wobei die Art der Klammer wirklich schwierig zu vermitteln ist:
Bleibt man in dieser Definition ist allerdings die Klammerung bei der for-Wiederholung schwierig. Denn in diesem Sinne wäre dann ‘for’ ein Funktionsname, (;;) eine Parameterliste, die hier allerdings mit ; statt mit , getrennt werden. Nur die {} Klammern passen noch.